Isomorphisms
When are two graphs
"the same"?
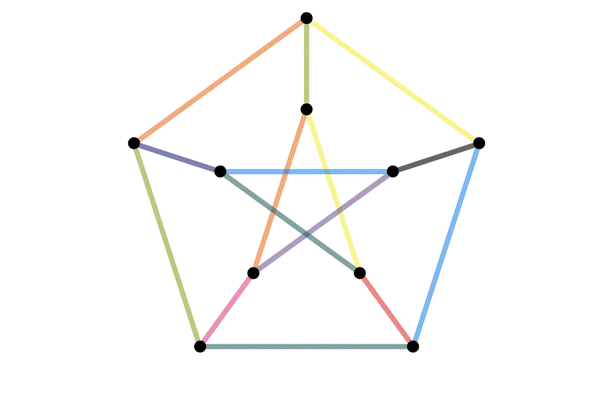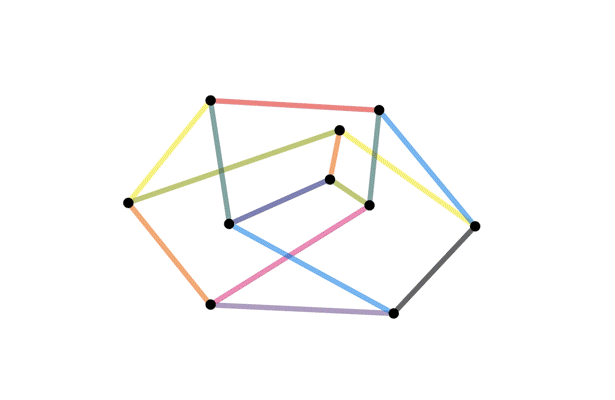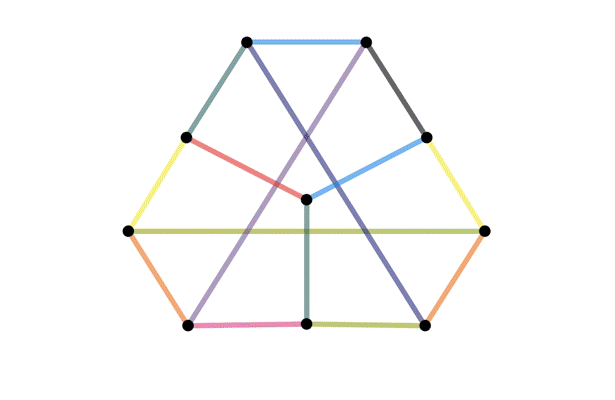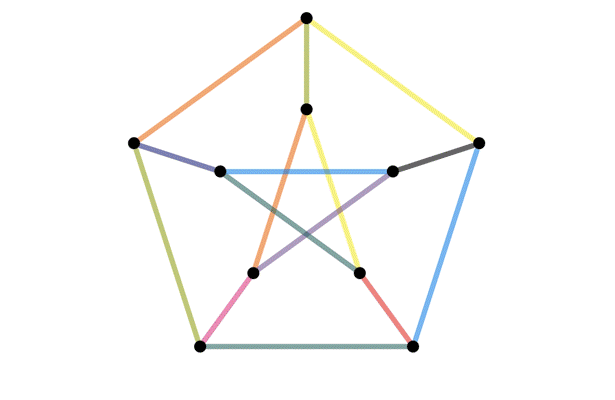
Definition of an isomorphism
An isomorphism $\varphi:G\to H$ of graphs is:
- A bijection $\varphi_V:V(G)\to V(H)$
- A bijection $\varphi_E:E(G)\to E(H)$
That "play nicely together", i.e.:
- We say $G$ and $H$ are isomorphic if there is an isomorphism between them.
- If $G$ and $H$ are simple, then $G$ and $H$ are isomorphic if and only if there is a bijection $\varphi$ between the vertices so that $\varphi(v)$ and $\varphi(w)$ are adjacent in $H$ if and only if $v$ and $w$ are adjacent in $G$.
The isomorphism problem:
Given two graphs $G$ and $H$, either find an isomorphism $\varphi:G\to H$, or prove such an isomorphism doesn't exist.
In general, this is a very important, deep and difficult question. In practice, it's not too bad for small graphs, and you will need to be able to do this for the exam.
How to prove two graphs are isomorphic?
Write down an isomorphism!
An obvious question...
How to write down an isomorphism?
- Usually not best to write down $\varphi_V$ as list
- Depends on how graphs are given to you
- If given as unlabeled drawings, easiest to redraw as given and record $\varphi_V$ by labeling graphs with same symbols
How to find an isomorphism?
One useful method -- expanding "local" isomorphisms.- Find a part $A\subset G$ that (would have to / could) map to a part $B\subset H$
- Things adjacent to $A$ need to map to things adjacent to $B$
- Continue expanding what we know of bijection
When graphs have symmetry, need to make an arbitrary choice to break the symmetry