Hand in any time before Easter break to have it marked for feedback; these questions do not count toward your final mark for the module.

This problem is, with minor adaptions, a question from the 2006 exam.

Part A (9 marks)

State Euler’s Theorem for plane graphs, and use it to show that if a \(G\) is a plane graph with no vertices of degree less than 3 or cycles with length less than 4, then \(G\) must have at least 8 vertices and at least 12 edges. Give an example to show that these bounds cannot be improved.

Part B (2 Marks)

Suppose that \(G\) is any graph with no vertices of degree less than 3 or cycles with length less than 4 – must \(G\) be planar? Justify your answer.

The rest of this question use the graph \(\Gamma\) show below.

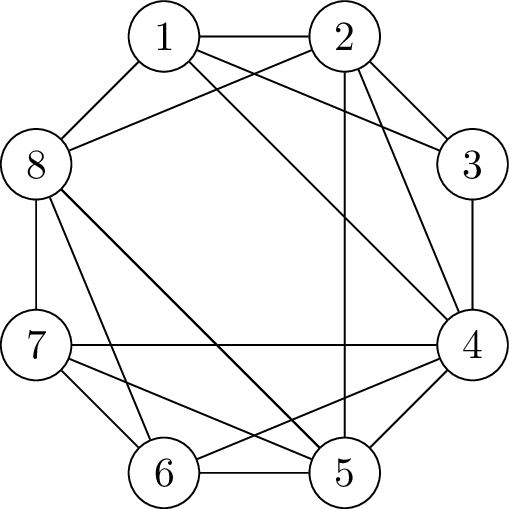
Part C (5 Marks)

Use the Planarity Algorithm for Hamiltonian Graphs (with the Hamiltonian cycle 123456781) to show that \(\Gamma\) is not planar.

Part D (5 Marks)

State Kuratowski’s Theorem, and use it to give another proof that \(\Gamma\) isn’t planar.

Part E (4 Marks)

Draw \(\Gamma\) on the torus so that no edges cross.