The field of graph theory arguably began with the following question.

The Bridges of Konigsberg

the city of Konigsberg (now Kaliningrad) was built on both sides of a river, and contained two large islands. The 4 sectors of the city were connected by seven bridges, as follows (picture from Wikipedia):

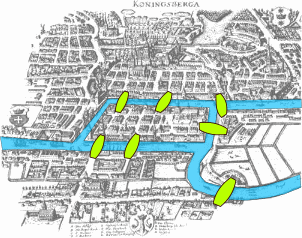
A group of friends enjoyed strolling through the city, and created a game: could they take a walk in the city, crossing every bridge exactly once, and return to where they started from? Eventually, Euler proved that such a walk is not possible, and in doing so founded graph theory.

Eulerian Cycles

Before presenting Euler’s proof, let us formulate the question precisely in terms of graph theory, which will also generalize the problem.

We can produce a graph $\Gamma_K$, which we will callt he Kingsberg graph, that represents the city of Konigsberg as follows. There will be four vertices, representing the four land-masses are vertices. Every bridge will be represented by an edge.

Then, the question reduces to finding a closed walk in the graph that will uses every edge exactly once. In particular, this walk will not use any edge more than once and hence will be a trail (though it may repeat vertices).

Definition: Eulerian cycle

Let $\Gamma$ be any graph. An Eulerian cycle or Eulerian tour is a walk in $\Gamma$ that visits every edge exactly once.

The citizens Konigsberg were asking whether an Eulerian cycle existed in $\Gamma_K$. Euler did more: he gave simple criterion to tell whether or not any connected graph $\Gamma$ has an Eulerian tour. We will now state and prove his result.

Theorem

A connected graph $\Gamma$ (without loops) has an Eulerian cycle if and only if every vertex of $\Gamma$ has even degree.

Proof

First, we show this condition is necessary. Let $\Gamma$ be a connected graph, and suppose that it has an Eulerian cycle $w=v_0, e_1, v_1,\dots, e_n, v_n$. Let $v$ be any vertex in $\Gamma$; we must show that $v$ has even degree. We will do this by pairing up the edges incident to $v$.

Since $w$ is a closed walked, we may assume that it does not start at $v$. Then consider the first time that the walk $w$ visits $v$ – it will enter by some edge $e_i$, and leave by some other edge $e_{i+1}$. We pair these two edges up.

The walk $w$ may visit $v$ multiple times; each time it does, it must enter from one edge, and leave from another edge. Each time the walk $w$ visits $e$, we will pair up the edge the walk $w$ entered with the edge $w$ left by. Since by supposition the walk $w$ uses every edge of $\Gamma$ exactly once, we see that every edge incident to $v$ will be paired up with exactly one other edge in this way, and hence $v$ must have even degree.

We now show that this condition is sufficient. That is, we suppose that every vertex of $\Gamma$ has even degree; we must show that $\Gamma$ has an Eulerian cycle. We will proceed by induction on the number of edges of $\Gamma$.

Any connected graph with 0 edges consists of just a vertex, and hence trivially has an Eulerian cycle.

Now, for the inductive step, we suppose that $\Gamma$ has $n$ edges, and further suppose that we know Euler’s theorem is true for all graphs with less than $n$ edges – that is, suppose that every connected graph $\Gamma$ with less than $n$ edges, all of whose vertices have even degree has an Eulerian walk.

We first claim that $\Gamma$ has some closed trail. Start at any vertex $v_0$. Since $\Gamma$ is connected, $v_0$ has at least one edge $e_1$ so we start our trail with $v_0, e_1, v_1$. Since every vertex has an even degree, there must be another edge out of $v_1$, say $e_2$ leading to $v_2$.

We continue building a trail in $\Gamma$ by randomly selecting an unused edge of $\Gamma$ at our current vertex. Since every vertex has even degree, and whenever our trail visits a vertex we use up edges two at a time (coming and going), we see that whenever we arrive at a vertex $v$, there must be another edge leaving it to continue our trail – unless perhaps we hit our starting vertex $v_0$, where we have only used one edge up. Thus, if we randomly start building a trail we must eventually return to our starting vertex and obtain a closed trail.

Now, given our graph $\Gamma$, we know it has some closed trail $w$. If $w$ uses every edge of $\Gamma$, we are done. If not, we consider the new graph $\Gamma^\prime$ obtained by deleting every edge of $w$ (but not the vertices). Note that every vertex of $\Gamma^\prime$ has even degree. Second, $\Gamma^\prime$ may not be connected, but each connected component $\Gamma_i^\prime$ of $\Gamma^\prime$ has fewer edges that $\Gamma$ and hence has an Eulerian tour $u_i$ by supposition. Together, $w$ and the $u_i$ visit every edge of $\Gamma$ exactly once. We can stitch them together into one closed path as follows – each $u_i$ shares at least one vertex $v_i$ with $w$. We trace the path $w$, but the first time we visit vertex $v_i$ we insert the path $u_i$ before continuing along $w$. $\square$