Definition

A forest is a graph with no cycles; a tree is a connected graph with no nontrivial closed trails.

Thus, a forest is a disjoint union of trees.

Example

The following graph is a forest consisting of three trees:

The following graph is a not a tree:

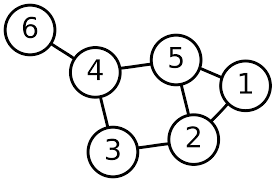
Consider the two conditions of being tree: being connected, and not having any cycles.

The first condition is somehow saying that $\Gamma$ has enough edges: to be connected, we need a path between any two vertices, and the more edges we have, the more likely this is to happen.

The second condition is somehow saying that $\Gamma$ doesn’t have too many edges: we don’t want cycles, and having more edges makes that more likely.

Thus, being a tree a bit of a goldilocks condition – it has just the right amount of edges. It’s not just how many edges the graph has, though – the path graph $P_4$ has 4 vertices and 3 edges, and is a tree, but the disjoint union of a triangle and a single vertex also has 4 vertices and 3 edges but is not a tree.

The following proposition summarises this discussion and makes it more precise:

Proposition

Let $\Gamma$ be a graph with $n$ vertices. The following are equivalent:

1. $\Gamma$ is a tree.
2. Between any two vertices $a,b\in V(\Gamma)$, there is a unique path.
3. $\Gamma$ is connected, but removing any edge makes $\Gamma$ disconnected.
4. $\Gamma$ has no cycles, but adding any edges to $\Gamma$ creates a cycle.
5. $\Gamma$ is connected and has $n-1$ edges
6. $\Gamma$ has no cycles and has $n-1$ edges

Proof:

We will not show all of the equivalences. Some are tricky to do directly; a few we will put on the practice sheet.

1 implies 3

Trees are by definition connected, so we must show that removing any edge of $\Gamma$ disconnects $\Gamma$. Let $a$ and $b$ be two adjacent vertices, and suppose removing the edge between them did not disconnect $\Gamma$. Then there is a path from $a$ to $b$ in $\Gamma$ not using the edge connecting them; adding the last edge back in makes a cycle, a condtradiction.

3 implies 2

Since $\Gamma$ is connected, there is at least one path between two vertices. If there were two paths between $a$ and $b$, then deleting any edge $e$ that was only in one of the paths wouldn’t disconnected $\Gamma$.

2 implies 1

Suppose that $\Gamma$ is a graph with a unique path between any two vertices. Then, in particular $\Gamma$ is connected, and so to show $\Gamma$ is a tree we must show it has no cycles.

Suppose $v_0, e_1, v_1,\dots, e_n, v_n=v_0$ was a cycle in $\Gamma$. Then there are two paths between $v_0$ and $v_1$ – the edge $e_1$, or the path $v_1, e_2, v_2,\dots, v_n=v_0$. This is a contradiction, and hence $\Gamma$ has no cycles.

We will also show that if $\Gamma$ is a tree with $n$ vertices, then $\Gamma$ has $n-1$ edges. Since we know trees are connected and have no cycles, this means any of 1-3 imply 5 and 6.

We proceed by induction: the proof is obvious when $n$ is one or two – a tree on one vertex has no edges, and a tree on two vertices has a single edge. Thus, we have a base case.

We now assume that all trees with at most $k$ vertices have $k-1$ edges for all $k<n$ and we must show that a tree with $n$ vertices has $n-1$ edges. Pick any edge $e$ of $\Gamma$ are remove it. By 3, the result $\Gamma\setminus e$ is disconnected.

We claim that $\Gamma\setminus e$ consists of exactly two connected components. Pick any two vertices $a,b\in\Gamma$. By 2, there is a unique path between them; if that path contains $e$, there will be no path between $a, b$ in $\Gamma\setminus e$, and hence they must lie in different components of $\Gamma\setminus e$. If the path between $a$ and $b$ does not contain $e$, then they will lie in the same component. Hence, if $v, w$ are the two ends of the edge $e$, then every vertex of $\Gamma\setminus e$ has a path to either $v$ or $w$, but not both.

Thus, we see $\Gamma\setminus e$ has two components $G_1$ and $G_2$, each of which are trees: they are connected, and have no cycles. Suppose $G_1$ contain $k$ vertices; then $G_2$ must have $n-k$ vertices. By the inductive hypothesis, we know they must contain $k-1$ edges and $n-k-1$ edges respectively.

The edges in $\Gamma$ are $e$ and the edges of $G_1$ and $G_2$, hence we see that $\Gamma$ has $1+(k-1)+(n-k-1)=n-1$ edges, as desired.