Connected components

Prove that for any graph $\Gamma$, there is a unique way to write $\Gamma$ as a dijoint union of connected subgraphs, up to reordering of the subgraphs. I.e., a unique way to write

where the $\Gamma_i$ are connected subgraphs. These subgraphs are called the connected components of $\Gamma$.

Counting paths

Let $\Gamma$ be the graph whose vertices are the 8 corners of the cube, and whose edges the 12 edges of the cube:

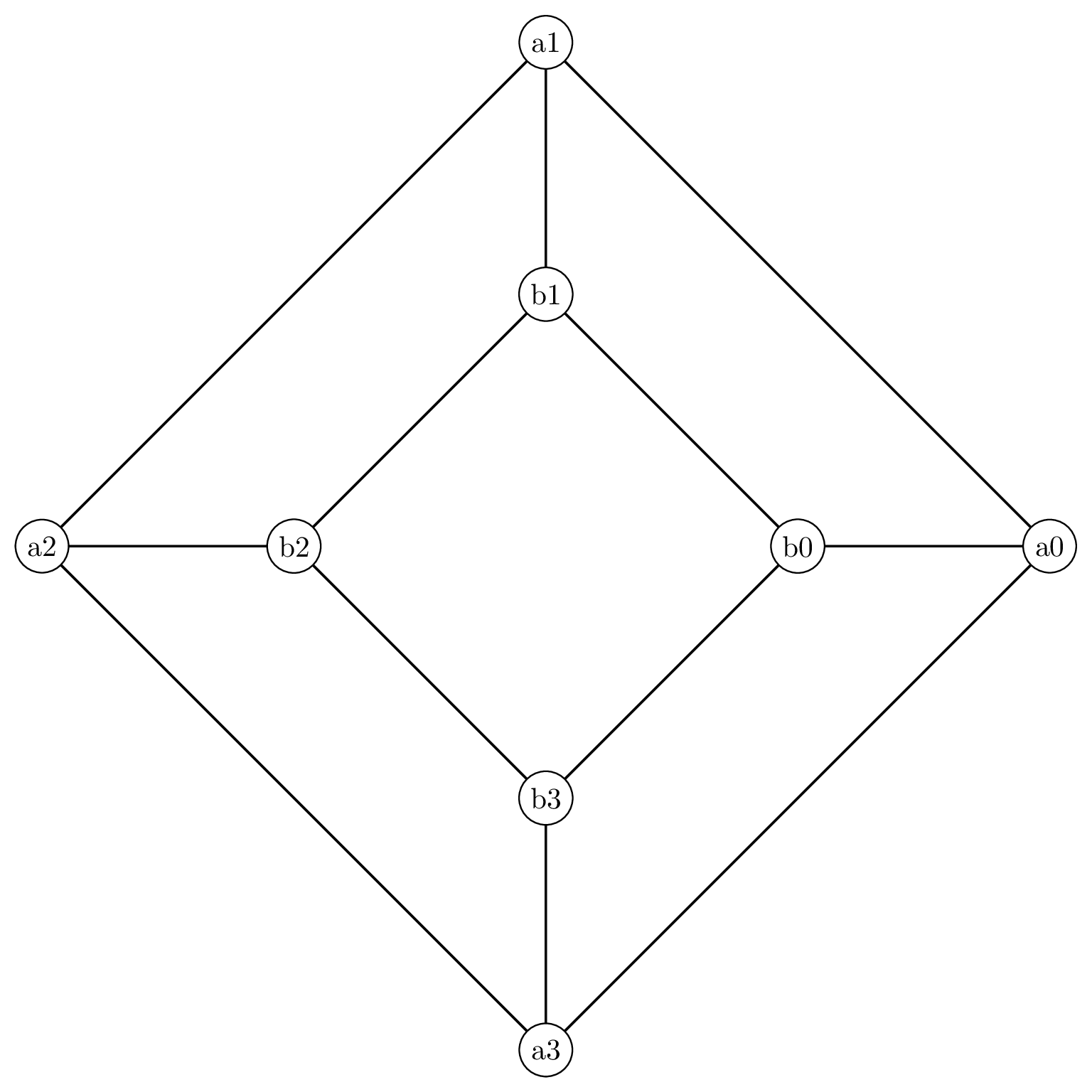
• How many walks of length three are there from one vertex of the cube to the opposite vertex of the cube – e.g., from a1 to b3.
• If we don’t fix the length of the walk, how many walks are there from a1 to b3?
• If we don’t fix the length, how many trails are there from a1 to b3?

Harder:

• If we don’t fix the length, how many paths are there from a1 to b3?

Project:

• How many walks of length $k$ are there from a1 to b3, for any $k$? (To do this, learn about eigenvalues of the adjacency matrix)

Finding an Eulerian cycle

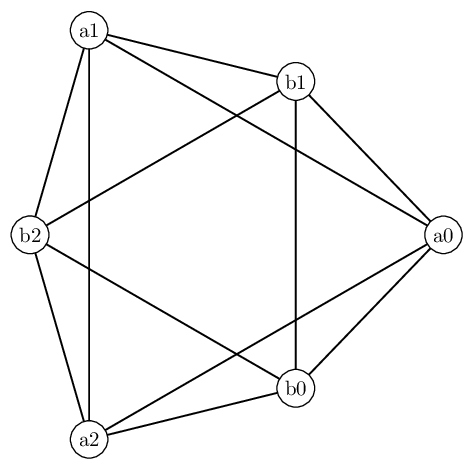
Find an Eulerian cycle in the following graph:

Connectedness and Eulerian cycles

We proved the theorem “A connected graph has an Eulerian cycle if and only if every vertex has even degree”, which is slightly different than “A graph has an Eulerian cycle if and only if it is connected and every vertex has an even degree”. Give an example to show that this second statement is false. (Hint: Any such example will necessarily be somewhat degenerate…)

Eulerian paths

An Eulerian path is a (not necessarily closed) path that uses every edge of $\Gamma$ exactly once. A graph is called semi-Eulerian if it has an Eulerian path.

Prove that a connected graph $\Gamma$ is semi-eulerian if and only if it has at most two vertices with odd degree.

Find an Eulerian path in each of the following graphs: