The icosian game

Hamilton marketed an ``icosian game’’, whose object was to find Hamiltonian cycles on various graphs. The base graph was the vertices an edges of a dodecahedron (as pictured below). Find a Hamiltonian cycle for that graph.

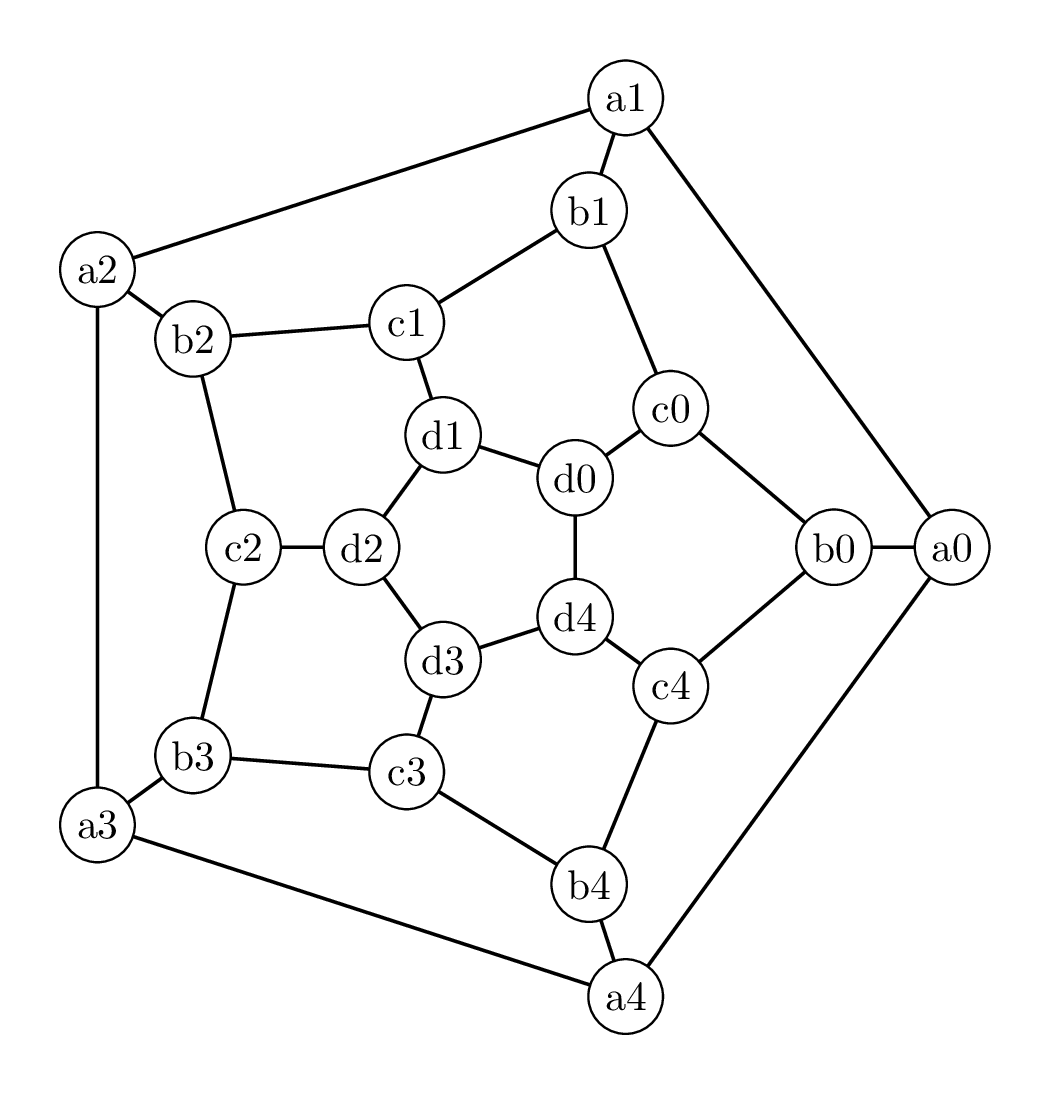
More challenging; prove that if we delete one vertex from this graph (say, a1) and the three edges adjacent to the vertex, the resulting graph with 19 vertices does not have a Hamiltonian cycle (some case by case analysis is needed).

More on finding Hamiltonian cycles or proving they don’t exist

Determine the number of Hamiltonian cycles in each of the following graphs. Two cycles count as the same if they use the same edges – starting at a different vertex or going backwards doesn’t make it different. Also, the answer may be zero.

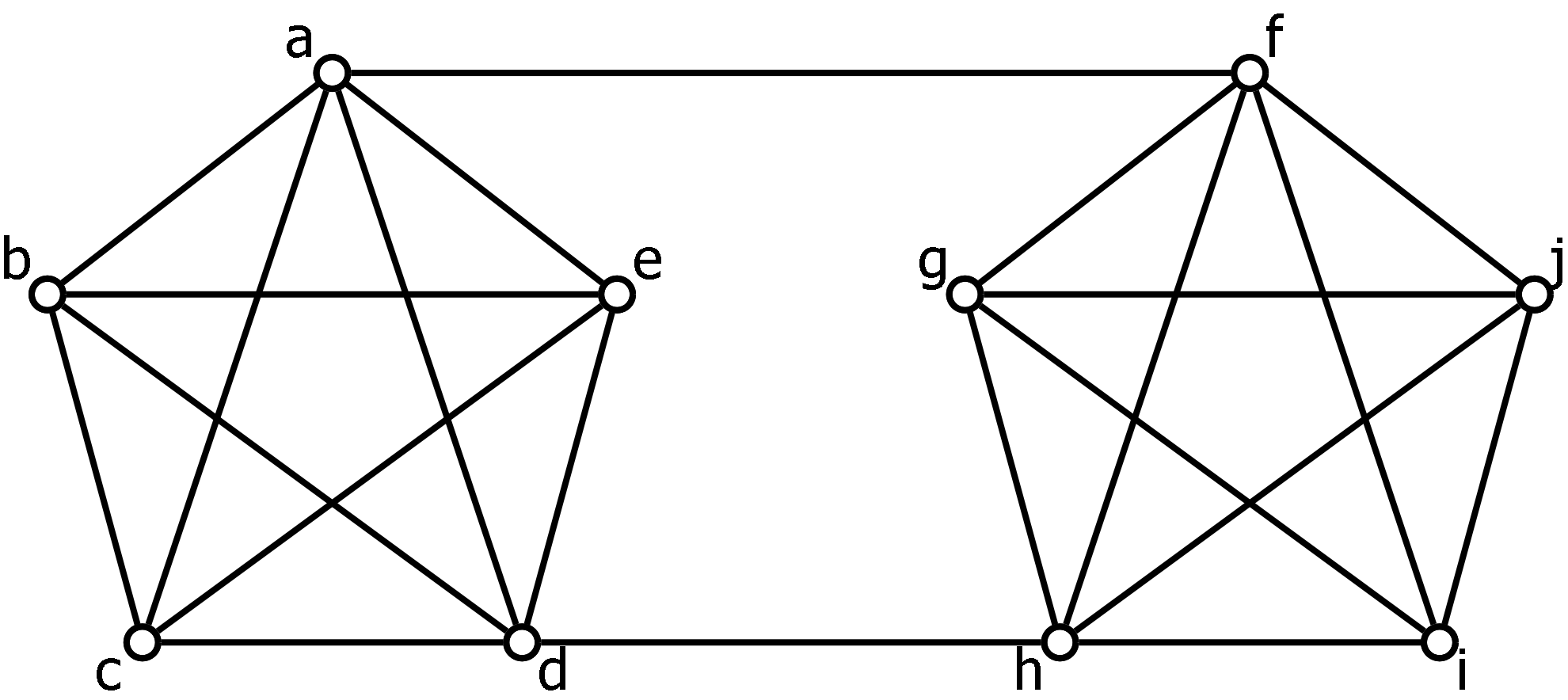
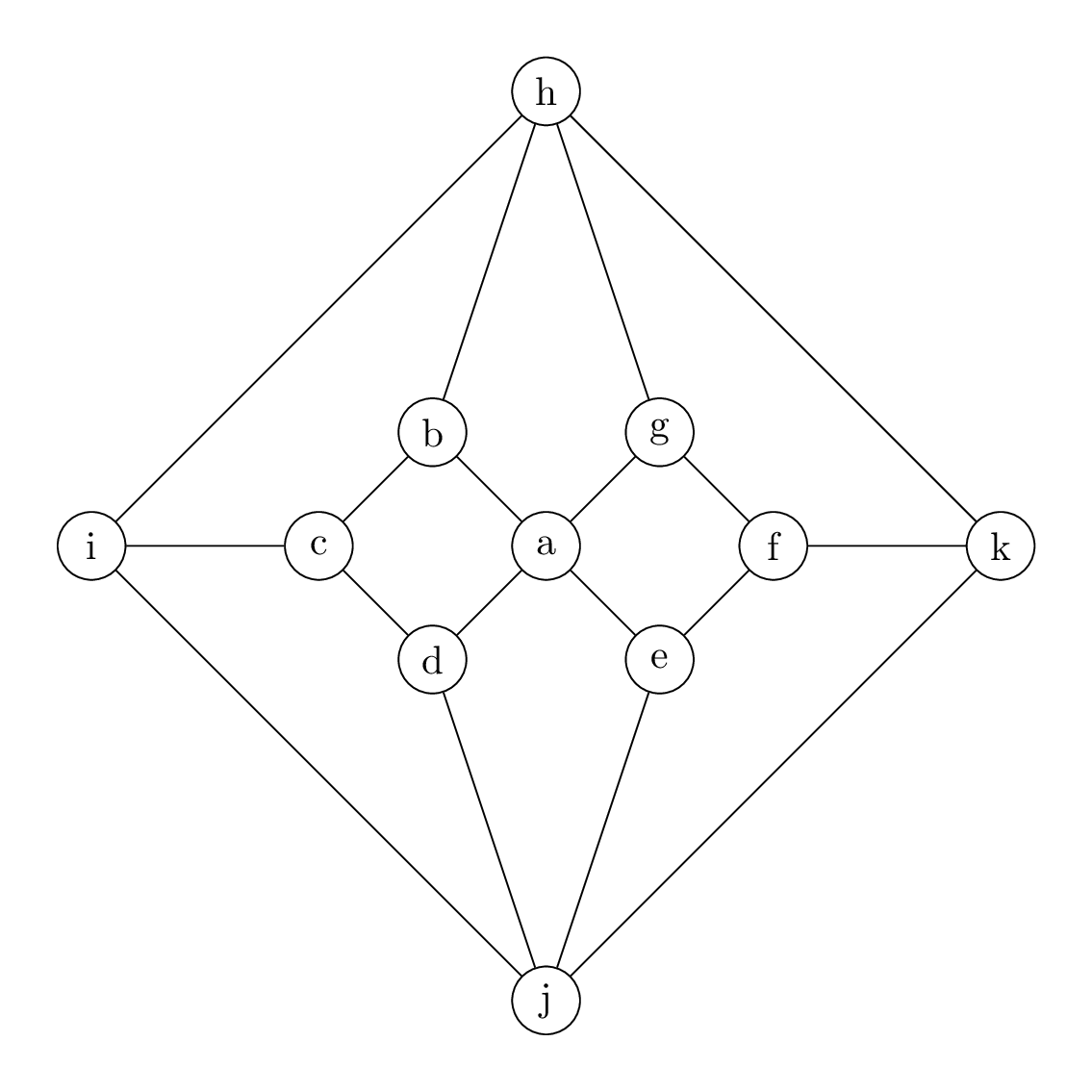
Hamiltonian cycles in Platonic solids

Show that that all the platonic solid graphs are Hamiltonian. How many Hamiltonian cycles in the tetrahedron? In the cube? Octahedron?