The most basic thing you have to do is either proof a graph is planar or not, and be able to draw graphs on other surfaces (the torus this week, and starting next week on the projective plane $\mathbb{RP}^2$ and the Klein Bottle).

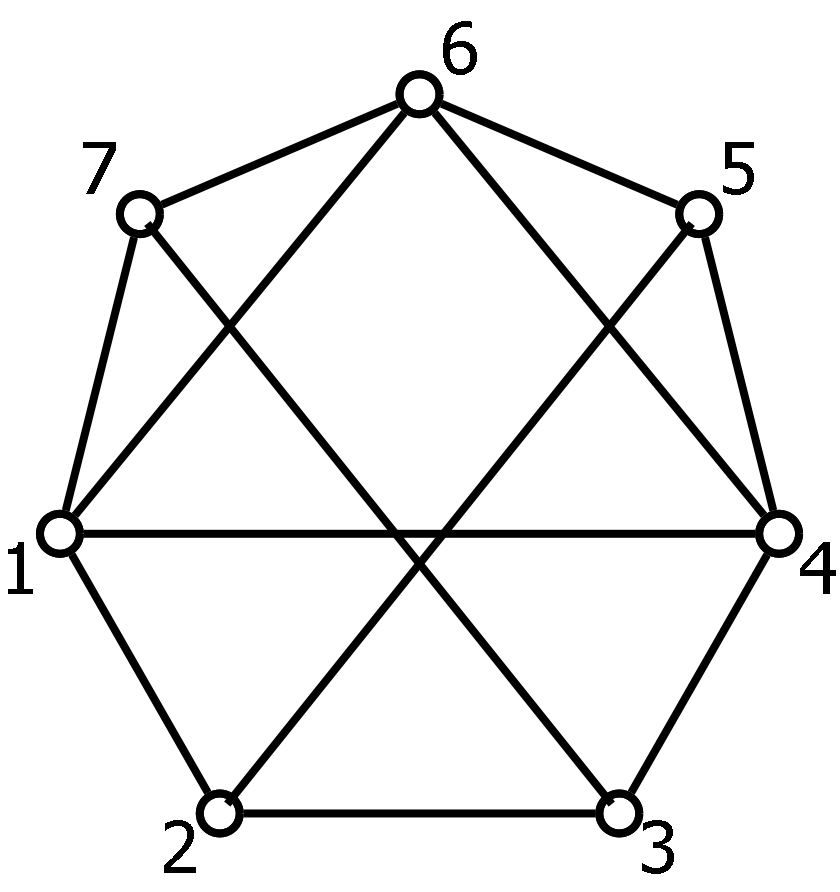
Example 1

Consider the graph $G$ below. Prove that $G$ is not planar by analysing whether edges go inside or outside a Hamiltonian cycle. Give another proof that it is not planar by using Kuratowski’s theorem. Finally, draw $G$ on the Torus and the real projective plane.

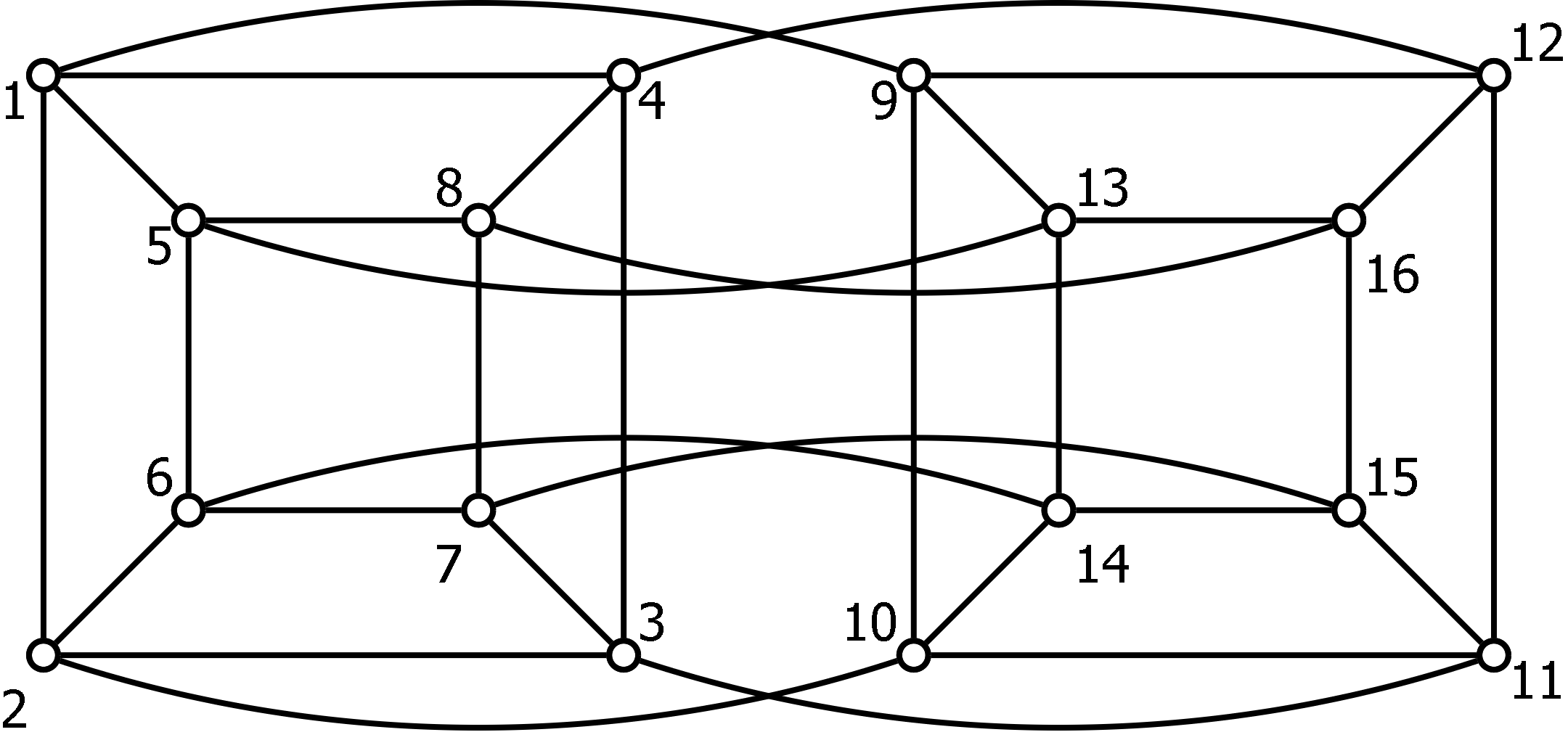
Example 2

A graph $H$ representing the edges of a 4-dimensional cube is shown below. Find a subgraph which is a subdivision of $K_{3,3}$, and another subgraph that is a subdivision of $K_5$, and thus determine that $H$ is nonplanar. Draw $H$ on the torus (being sure to label the vertices).