MAS341

Graph Theory

Lecture 1

Paul Johnson

Basic Information

Contact

  • Website is on Blackboard
  • Email: paul.johnson@sheffield.ac.uk
  • Office hours: Friday 2:00-3:00 Hicks J06b
  • Or: Email for an appointment, or after class

Marking

  • The final exam is 100% of the grade :(
  • Should be very similar to previous years' exams
  • Old exams and solutions available
  • Homeworks are 'exam type' questions

Fun Survey Course

  1. Introduction and paths (6 lectures)
  2. Algorithms (4 lectures)
  3. Graphs on Surfaces (4 lectures)
  4. Colouring Graphs (4 lectures)
  5. Bonus material + review sessions (2 lectures + extra)

Miss a lecture for a bank holiday, leaving one lecture overrun

Notes and Lectures

  • Notes for module cover same content as lecture
  • Different presentation: lecture and reading different mediums
  • Lectures recorded on Encore, but miss chalkboard...
  • Better using recordings from pandemic
...the first duty of a lecturer -- to hand you after an hour's discourse a nugget of pure truth to wrap up between the pages of your notebooks and keep on the mantel-piece for ever

Virginia Woolf, A Room of One's Own

Examples and definition

Graphs encode:

Connections (edges)

between

things (vertices)

Formal Definition

A simple graph $\Gamma$ consists of:

  • A set $V(\Gamma)$ of vertices
  • A set $E(\Gamma)$ of edges of the two element subsets of $V(\Gamma)$

For $e\in E(\Gamma), e=\{v_1,v_2\}$, then $e$ "connects" $v_1$ and $v_2$

Some consequences:

Following from our choice of formal definition:

  • The edges are symmetrical -- Facebook, not Twitter
  • No loops, i.e. edges connecting a vertex to itself
  • No multiple edges between the same pair of vertices

      • Generally, "graph" will mean "simple graph", but sometimes we will consider non-simple graphs.

First application

Suppose you are at a party with 6 other people.

Is it possible that every person knows exactly three other people at the party?

(It is assumed if $A$ knows $B$, then $B$ knows $A$).

Make it a graph

  • Vertices are people (so there are 7)
  • Edge between two people if they know each other

Since each person knows three people, there are three edges coming out of each vertex

Try to draw such a graph

Avoiding a case by case proof

Suppose everyone shook hands with the people at the party they knew. How many handshakes would occur?

Two ways to count handshakes:

  • Each edge is a pair of people who know each other. So there will be $|E(\Gamma)|$ handshakes.
  • Since everyone knows three people, everyone will be involved in three handshakes. But each handshake involves two people. So, by this count, there would be $7\cdot 3/2=10.5 $ handshakes, i.e., edges, which is obviously nonsense

A generalization

Definition:

For a simple graph $\Gamma$, and $v\in V(\Gamma)$, the degree of $v, d(v)$, is the number of vertices adjacent to $v$.

Euler's handshaking Lemma

$$\sum_{v\in V(\Gamma)}d(v)=2|E(\Gamma)|$$

The degree sequence

The degree sequence of a graph is just the list of degrees of the vertices, with multiplicity.

Degree sequence in Chemistry

Covalent Bonds

  • Hydrogen (H) and Fluorine (F) have degree 1
  • Oxygen (O) and Sulfur (S) have degree 2
  • Nitrogen (N) and Phosphorous (P) have degree 3
  • Carbon (C) has degree 4

In biochemistry, carbon and hydrogen are most common. Carbon are left blank, and Hydrogen aren't drawn at all

Fluoxetine (Prozac)

Hydrocarbons

An application

Instant Insanity

  • 4 cubes
  • Each side of each cube is colored one of four colors
  • Goal is to stack cubes so each direction has all 4 colours
  • Patterns online to make your own cubes and try to solve

Isomorphisms

When are two graphs

"the same"?

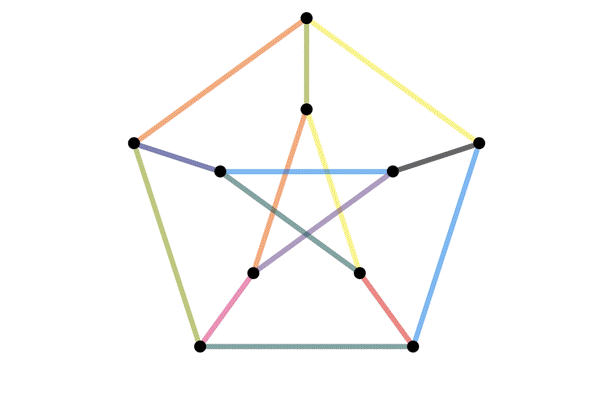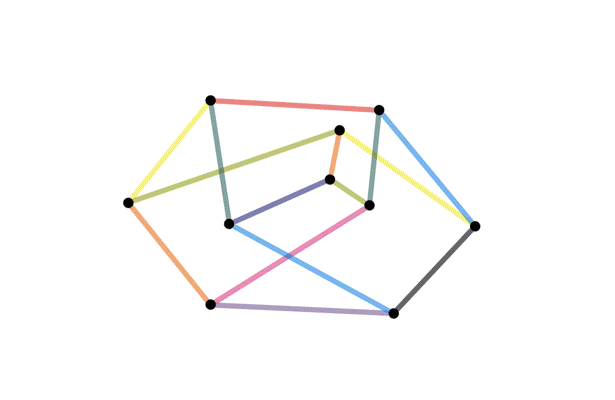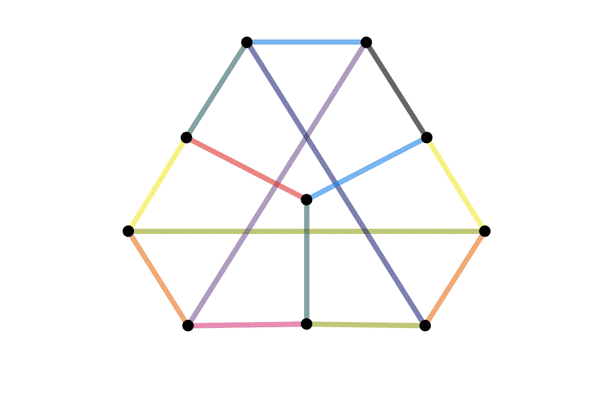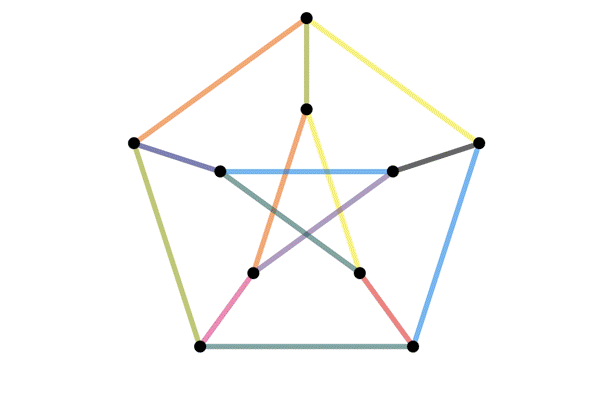
Definition of an isomorphism

An isomorphism $\varphi:G\to H$ of graphs is:

  • A bijection $\varphi_V:V(G)\to V(H)$
  • A bijection $\varphi_E:E(G)\to E(H)$

That "play nicely together", i.e.:

If $e\in E(G)$ connects $u$ and $v$, then $\varphi_E(e)\in E(H)$ connects $\varphi_V(u)$ and $\varphi_V(v)$.
  • We say $G$ and $H$ are isomorphic if there is an isomorphism between them.
  • If $G$ and $H$ are simple, then $G$ and $H$ are isomorphic if and only if there is a bijection $\varphi$ that preserves the number of edges between vertices; that is, so that $\varphi(v)$ and $\varphi(w)$ are adjacent if and only if $v$ and $w$ were adjacent.
  • This breaks down if $G$ and/or $H$ have multiple edges. (why?)
  • Our original definition of isomorphism is arguably slightly wrong if $G$ and $H$ have loops. (Why?)