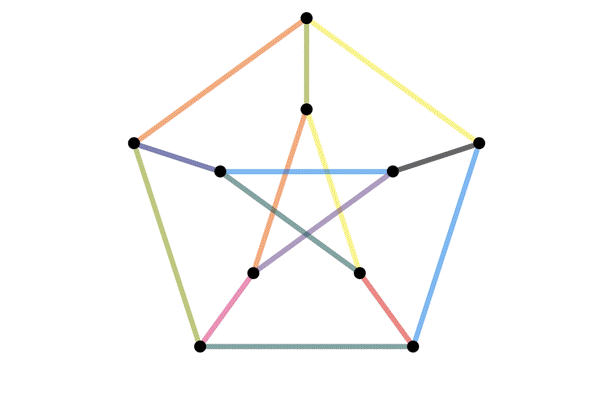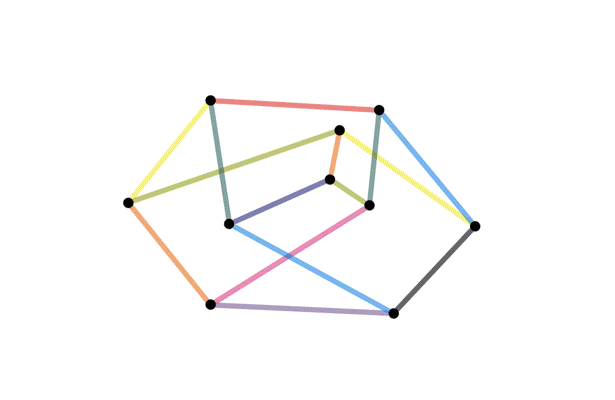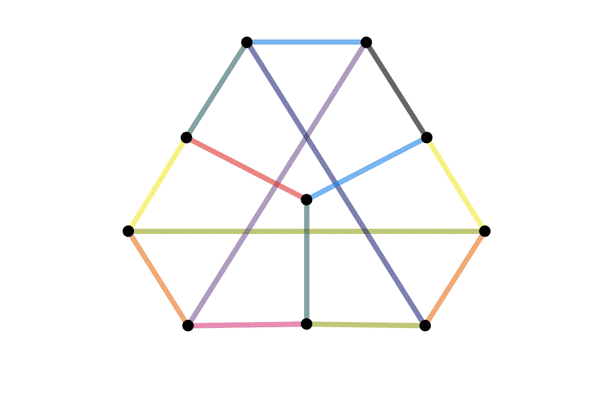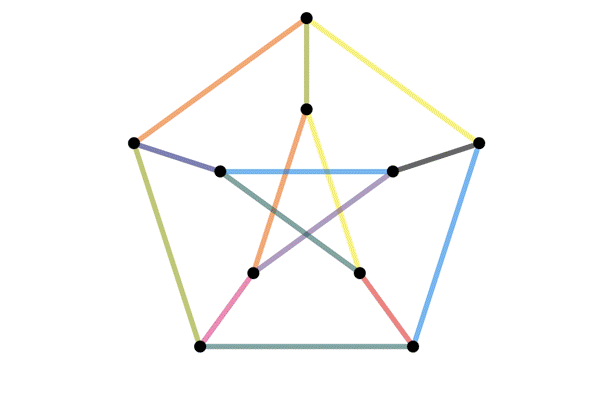
Definition of an isomorphism

An isomorphism $\varphi:G\to H$ of graphs is:

A bijection $\varphi_V:V(G)\to V(H)$
A bijection $\varphi_E:E(G)\to E(H)$

That "play nicely together", i.e.:

$e\in E(G)$ connects

$u$ and

$v$ , then

$\varphi_E(e)\in E(H)$ connects

$\varphi_V(u)$ and

$\varphi_V(v)$ .

We say $G$ and $H$ are isomorphic if there is an isomorphism between them.
If $G$ and $H$ are simple, then $G$ and $H$ are isomorphic if and only if there is a bijection $\varphi$ that preserves the number of edges between vertices; that is, so that $\varphi(v)$ and $\varphi(w)$ are adjacent if and only if $v$ and $w$ were adjacent.
This breaks down if $G$ and/or $H$ have multiple edges. (why?)
Our original definition of isomorphism is arguably slightly wrong if $G$ and $H$ have loops. (Why?)

The isomorphism problem:

Given two graphs $G$ and $H$ , either find an isomorphism $\varphi:G\to H$ , or prove such an isomorphism doesn't exist.

In general, this is a very important, deep and difficult question. In practice, it's not too bad for small graphs, and you will need to be able to do this for the exam.

A little mathematical culture

The isomorphism problem is of fundamental importance to theoretical computer science.

Practical applications
It's in NP, but not known to be NP complete or in P

How to prove two graphs are isomorphic?

Write down an isomorphism!

An obvious question...

How to write down an isomorphism?

Usually not best to write down $\varphi_V$ as list
Depends on how graphs are given to you
If given as unlabeled drawings, easiest to redraw as given and record $\varphi_V$ by labeling graphs with same symbols

How to find an isomorphism?

One useful method -- expanding "local" isomorphisms.

Find a part $A\subset G$ that (would have to / could) map to a part $B\subset H$
Things adjacent to $A$ need to map to things adjacent to $B$
Continue expanding what we know of bijection

If graphs are symmetric, need to make an arbitrary choice to break the symmetry

Graph Theory Lecture 2:

Isomorphisms