If the edges in a graph $\Gamma$ represent connections, it is obvious to ask whether $\Gamma$ as a whole is “connected”. There are two seemingly different ways of making this precise; today we introduce these and show that they are the same.

It may be easiest to define what it means for a graph $\Gamma$ to be disconnected.

Definition: Disjoint union

Given two graphs $\Gamma_1$ and $\Gamma_2$, the disjoint union $\Gamma_1\sqcup \Gamma_2$ is obtained by taking the disjoint union of both the vertices and edges of $\Gamma_1$ and $\Gamma_2$. So $\Gamma_1\sqcup\Gamma_2$ consists of a copy of $\Gamma_1$ and a copy of $\Gamma_2$, with no edges in between the two graphs.

Definition: Disconnected

A graph $\Gamma$ is disconnected if we can write $\Gamma=\Gamma_1\sqcup \Gamma_2$ for two proper (i.e., not all of $\Gamma$) subgraphs $\Gamma_1$ and $\Gamma_2$.

It then makes sense to say that $\Gamma$ is connected if it is not disconnected. However, the more intuitive notion of being connected is that “you can get from any vertex to any other”, which we now make precise.

Walks, Trails, Paths

Definition

A walk in a graph $\Gamma$ is a sequence

where

• the $v_i$ are vertices
• the $e_j$ are edges
• edge $e_j$ goes between vertices $v_{j-1}$ and $v_j$

Note that, when the graph $\Gamma$ does not have multiple edges, it is enough to record just the $v_i$, but if $\Gamma$ has multiple edges that just knowing the vertices does not determine the walk.

We say that the walk is between vertices $a$ and $b$ if $a=v_0$ to vertex $b=v_n$. Thus, it is natural to say that a graph $\Gamma$ is connected if there is a walk between any two vertices $a,b\in\Gamma$. We now show that this agrees with our previous definition of connected.

Lemma

The following are equivalent:

1. $\Gamma$ is connected.
2. There is a walk between any two vertices $v, w\in V(\Gamma)$

Proof

1 implies 2: Supppose that $\Gamma$ is connected, and let $v, w\in V(\Gamma)$; we want to show that there is a walk from $v$ to $w$.

Define $S\subset V(\Gamma)$ to be the set of all vertices $u\in V(\Gamma)$ so that there is a walk from $v$ to $u$; we want to show that $w\in S$.

First, observe that there are no edges from $S$ to $V(\Gamma)\setminus S$. Suppose that $e$ was an edge between $a\in S$ and $b\in\Gamma\setminus S$. Since $a\in S$, by the definition of $S$ there is a walk $v=v_0v_1v_2\cdots v_m=a$ from $v$ to $a$. We can add the edge $e$ to the end of the walk, to get a walk from $v$ to $b$, and hence by definition $b\in S$.

Now suppose that $w\notin S$. Then $S$ and $V(\Gamma)\setminus S$ are both nonempty, and by the above there are no edges between them, and so $\Gamma$ is not connected, a contradiction.

To prove 2 implies 1, we prove the contrapositive. If $\Gamma$ is not connected, then there are two vertices $v,w\in V(\Gamma)$ so that there is no walk from $v$ to $w$.

Suppose that $\Gamma=\Gamma_1\sqcup\Gamma_2$, and pick $v\in V(\Gamma_1), w\in V(\Gamma_2)$. Any walk from $v$ to $w$ starts in $V(\Gamma_1)$ and ends in $V(\Gamma_2)$, and so at some point there must be an edge from a vertex in $\Gamma_1$ to a vertex in $\Gamma_2$, but there are no such edges $\square$

Types of Walks

Many questions in graph theory ask whether or not a walk of a certain type exists on a graph: we introduce some notation that will be needed for these questions.

We say a walk is closed if it starts and ends on the same vertex; i.e., $v_0=v_n$. The length of a walk is $n$, the number of edges in it. The distance between two vertices $v$ and $w$ is the length of the shortest walk from $v$ to $w$, if one exists, and $\infty$ if one does not exist.

Walks, trails and paths

• If the edges $e_i$ of the walk are all distinct, we call it a trail
• If the vertices $v_i$ of the walk are all distinct (except possibly $v_0=v_m$), we call the walk a path. The exception is to allow for the possibility of closed paths.

Lemma

Let $v,w\in V(\Gamma)$. The following are equivalent:

1. There is a walk from $v$ to $w$.
2. There is a trail from $v$ to $w$
3. There is a path from $v$ to $w$.

Proof

Obviously, 3 implies 2 which implies 1, as any path is a trail, and any trail is a walk.

That 1 implies 3 is intuitively obvious: if you repeat a vertex, then you’ve visited someplace twice, and weren’t taking the shortest route. Let’s make this argument mathematically precise.

Suppose we have a walk $v=v_0,e_1,\dots, e_m, v_m=w$ that is not a path. Then, we must repeat some vertex, say $v_i=v_k$, with $i<k$. Then we can cut out all the vertices and edges between $v_i$ and $v_k$ to obtain a new walk

$v=v_0,e_1, v_1,\dots, e_i, v_i, e_{k+1}, v_{k+1}, e_{k+2}, v_{k+2}, \dots, v_m$.

Since $i<k$, the new walk is strictly shorter than our original walk. Since the length of a walk is finite, if we iterate this process the result must eventually terminate. That means all our vertices are distinct, and hence is a path. $\square$

The field of graph theory arguably began with the following question.

The Bridges of Konigsberg

the city of Konigsberg (now Kaliningrad) was built on both sides of a river, and contained two large islands. The 4 sectors of the city were connected by seven bridges, as follows (picture from Wikipedia):

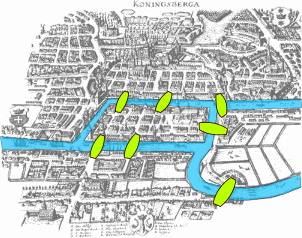
A group of friends enjoyed strolling through the city, and created a game: could they take a walk in the city, crossing every bridge exactly once, and return to where they started from? Eventually, Euler proved that such a walk is not possible, and in doing so founded graph theory.

Eulerian Cycles

Before presenting Euler’s proof, let us formulate the question precisely in terms of graph theory, which will also generalize the problem.

We can produce a graph $\Gamma_K$, which we will callt he Kingsberg graph, that represents the city of Konigsberg as follows. There will be four vertices, representing the four land-masses are vertices. Every bridge will be represented by an edge.

Then, the question reduces to finding a closed walk in the graph that will uses every edge exactly once. In particular, this walk will not use any edge more than once and hence will be a trail (though it may repeat vertices).

Definition: Eulerian cycle

Let $\Gamma$ be any graph. An Eulerian cycle or Eulerian tour is a walk in $\Gamma$ that visits every edge exactly once.

The citizens Konigsberg were asking whether an Eulerian cycle existed in $\Gamma_K$. Euler did more: he gave simple criterion to tell whether or not any connected graph $\Gamma$ has an Eulerian tour. We will now state and prove his result.

Theorem

A connected graph $\Gamma$ (without loops) has an Eulerian cycle if and only if every vertex of $\Gamma$ has even degree.

Proof

First, we show this condition is necessary. Let $\Gamma$ be a connected graph, and suppose that it has an Eulerian cycle $w=v_0, e_1, v_1,\dots, e_n, v_n$. Let $v$ be any vertex in $\Gamma$; we must show that $v$ has even degree. We will do this by pairing up the edges incident to $v$.

Since $w$ is a closed walked, we may assume that it does not start at $v$. Then consider the first time that the walk $w$ visits $v$ – it will enter by some edge $e_i$, and leave by some other edge $e_{i+1}$. We pair these two edges up.

The walk $w$ may visit $v$ multiple times; each time it does, it must enter from one edge, and leave from another edge. Each time the walk $w$ visits $e$, we will pair up the edge the walk $w$ entered with the edge $w$ left by. Since by supposition the walk $w$ uses every edge of $\Gamma$ exactly once, we see that every edge incident to $v$ will be paired up with exactly one other edge in this way, and hence $v$ must have even degree.

We now show that this condition is sufficient. That is, we suppose that every vertex of $\Gamma$ has even degree; we must show that $\Gamma$ has an Eulerian cycle. We will proceed by induction on the number of edges of $\Gamma$.

Any connected graph with 0 edges consists of just a vertex, and hence trivially has an Eulerian cycle.

Now, for the inductive step, we suppose that $\Gamma$ has $n$ edges, and further suppose that we know Euler’s theorem is true for all graphs with less than $n$ edges – that is, suppose that every connected graph $\Gamma$ with less than $n$ edges, all of whose vertices have even degree has an Eulerian walk.

We first claim that $\Gamma$ has some closed trail. Start at any vertex $v_0$. Since $\Gamma$ is connected, $v_0$ has at least one edge $e_1$ so we start our trail with $v_0, e_1, v_1$. Since every vertex has an even degree, there must be another edge out of $v_1$, say $e_2$ leading to $v_2$.

We continue building a trail in $\Gamma$ by randomly selecting an unused edge of $\Gamma$ at our current vertex. Since every vertex has even degree, and whenever our trail visits a vertex we use up edges two at a time (coming and going), we see that whenever we arrive at a vertex $v$, there must be another edge leaving it to continue our trail – unless perhaps we hit our starting vertex $v_0$, where we have only used one edge up. Thus, if we randomly start building a trail we must eventually return to our starting vertex and obtain a closed trail.

Now, given our graph $\Gamma$, we know it has some closed trail $w$. If $w$ uses every edge of $\Gamma$, we are done. If not, we consider the new graph $\Gamma^\prime$ obtained by deleting every edge of $w$ (but not the vertices). Note that every vertex of $\Gamma^\prime$ has even degree. Second, $\Gamma^\prime$ may not be connected, but each connected component $\Gamma_i^\prime$ of $\Gamma^\prime$ has fewer edges that $\Gamma$ and hence has an Eulerian tour $u_i$ by supposition. Together, $w$ and the $u_i$ visit every edge of $\Gamma$ exactly once. We can stitch them together into one closed path as follows – each $u_i$ shares at least one vertex $v_i$ with $w$. We trace the path $w$, but the first time we visit vertex $v_i$ we insert the path $u_i$ before continuing along $w$. $\square$

Hamiltonian Cycles

Definition

A graph $\Gamma$ is Hamilton if there exists a closed walk that visits every vertex exactly once.

Although the definition of a Hamiltonian graph is extremely similar to an Eulerian graph, it is much harder to determine whether a graph is Hamiltonian or not: doing so is an NP-complete problem.

Examples

Proposition

The Petersen graph is not Hamiltonian.

Proof

Suppose the Petersen graph was Hamiltonian, and let $v_0-v_1-v_2-v_3-\cdots-v_{9}-v_0$ denote the Hamiltonian cycle, as we have drawn below:

The Petersen graph has 15 edges, and the Hamiltonian cycle uses 10 of them, so there must be 5 edges left in the Petersen graph that are not in the Hamiltonian cycle. The proof works by considering the possibilities for these 5 extra edges.

Let us consider the extra edge incident to $v_0$; the others are equivalent. Since the Petersen graph has no loops or multiple edges, this edge cannot go from $v_0$ to itself, or to $v_1$ or $v_9$.

Since the Petersen graph has no triangles or 4 cycles, this edge cannot “skip” 1 or 2 vertices in the Hamiltonian cycle. More specifically, we cannot we cannot have an edge from $v_0$ to $v_2$ or $v_8$, as these make triangles, as in the dashed edges below:

And we cannot have edges $v_0$ to $v_3$ or to $v_7$, as these make 4 cycles:

Thus, the only possibility for these edges is that they “skip” 4 or 5 vertices (skipping more than 5 vertices is the same as skipping less vertices in the other direction). So for instance, $v_0$ can only be connected to $v_4, v_5$ or $v_6$ with its extra edge.

We now claim that at least one of these extra edges must “skip” 4 vertices. If not, then every extra edge would skip 5 vertices. Since each vertex has degree 3, there must be one extra edge through each of these vertices, connecting to the opposite vertex. But this configuration has many four cycles – for instance, $v_0-v_1-v_6-v_5-v_0$. Since the Petersen graph does not have any 4 cycles, we see this cannot occur:

Relabeling our edges if necesary, we can make the extra edge that skips the 4 cycle be the edge $v_0-v_4$. Now, consider the extra edge at $v_5$. This cannot skip 5, because that would make it adjacent to $v_0$, which already has its extra edge. Thus, it must skip 4, and be adjacent to either $v_9$ or $v_1$. But since each of these are adjacent to $v_0$, it would create a 4-cycle: either $v_0-v_4-v_5-v_9-v_0$, or $v_0-v_4-v_5-v_1-v_0$.

We have drawn the edge from $v_0$ to $v_4$ in solid red; any of the dashed edges from $v_5$ create a configuration not found in the Petersen graph:

$\square$

Partial results on Hamiltonian graphs

Although there is no complete characterisation of Hamiltonian graphs, there are several nice sufficient conditions for a graph to be Hamiltonian;

Ore’s Theorem

Let $\Gamma$ be a simple graph with $n$ vertices such that for any two nonadjacent vertices $v$ and $w$, we have $\text{deg}(v)+\deg{w}\geq n$. Then $\Gamma$ is Hamiltonian.

Proof

We will give a proof by contradiction. First, suppose that $\Gamma$ were a counterexample. Adding edges to $\Gamma$ preserves the condition on the degrees, and so we may continually add edges to $\Gamma$ until adding any more would create a Hamiltonian cycle. We will thus assume that $\Gamma$ is a counterexample with the maximal set of edges.

The benefit of this is that such a $\Gamma$ must have a non-closed path that visits every vertex exactly once. To see this, add one more edge $e$ to $\Gamma$ – the resulting graph then has a Hamiltonian cycle, which must pass through $e$, deleting $e$ give the desired path.

Let $v_1-v_2-\dots v_{n-1}-v_n$ be the path visiting every vertex of $\Gamma$. We will complete the proof by showing there exists an $i\in 3,\cdots, n-1$ so that $v_1$ is adjacent to $v_i$ and $v_n$ is adjacent to $v_{i-1}$. This completes the proof because $v_1-v_2-\cdots v_{i-1}-v_n-v_{n-1}-v_{n-2}-\dots v_i-v_1$ is a Hamiltonian path. We illustrate this below, with $n=9$ and $i=5$:

The existence of such an $i$ follows from the pigeon hole principle. Since $v_1$ and $v_n$ are not adjacent by supposition, the sum of their degrees is at least $n$. Two edges incident to them are accounted for $v_1-v_2$, and $v_{n-1}-v_{n-2}$, so there must be at least $n-2$ other edges incident to $v_1$ or $v_{n}$. Since $\Gamma$ is simple, any such edge out of $v_1$ has $n-3$ possibilities: $v_3, v_4, \dots, v_{n-1}$. Similarly, there are $n-3$ possibilities for an edge adjacent to $v_n$ – $v_2,v_3,\dots, v_{n-2}$. We pair these edges up into the possibilities we want, creating $n-3$ bins. Since there are $n-2$ edges we need to distribute among these bins, one of the bins must contain at least two, which is exactly what we needed to show.