Exercises

Exercises 5.5 Exercises

1.

Eleven football games are to be arranged among eight teams A to H as follows.

\begin{equation*} \begin{array}{l|l|l} A \text{ plays } F,G,H \amp D \text{ plays } C,E,G \amp F \text{ plays } H \\ B \text{ plays } E,F,H \amp E \text{ plays }G \amp \end{array} \end{equation*}

If no team can play more than once a week, what is the minimum number of weeks needed to schedule all the games? Justify your answer.

2.

Eight students A--H each have to choose two courses from a list of eight options 1--8. They choose as follows.

\begin{equation*} \begin{array}{llll} A : 1,2\qquad \amp B : 2,6 \qquad \amp C : 3,5\qquad \amp D : 4,6 \\ E : 5,7 \amp F : 7,8 \amp G : 5,8 \amp H : 3,8 \end{array} \end{equation*}

You have to timetable the examinations in such a way that no student has to take two exams on the same day. What is the smallest number of days you need, and in how many ways can you fit the exams into these days? Describe one way.

3.

Eight foods A to H are to be put in refrigerated compartments in a supermarket. Because of various regulations, some cannot share the same compartment with others, as indicated by crosses in the following table.

\begin{equation*} \begin{array}{cccccccc} A \amp \times \amp -- \amp -- \amp \times \amp \times \amp -- \amp \times \\ \amp B \amp \times \amp -- \amp -- \amp \times \amp -- \amp \times \\ \amp \amp C \amp \times \amp -- \amp \times \amp \times \amp \times \\ \amp \amp \amp D \amp \times \amp \times \amp \times \amp -- \\ \amp \amp \amp \amp E \amp \times \amp \times \amp -- \\ \amp \amp \amp \amp \amp F \amp -- \amp -- \\ \amp \amp \amp \amp \amp \amp G \amp \times \\ \amp \amp \amp \amp \amp \amp \amp H \end{array} \end{equation*}

Determine the smallest number of compartments needed to display the foods and find a possible placing of the foods in the compartments.

4.

For the graph \(\bfG\) shown below, find \(\chi(\bfG)\) and \(\chi^\prime(\bfG)\)

Figure 5.5.1. The graph \(\bfG\)

5.

Find the chromatic polynomial of the following three graphs. You should use the chromatic polynomial of the four cycle as a given: \(\chi_{C_4}(k)=k(k-1)(k^2-3k+3)\)

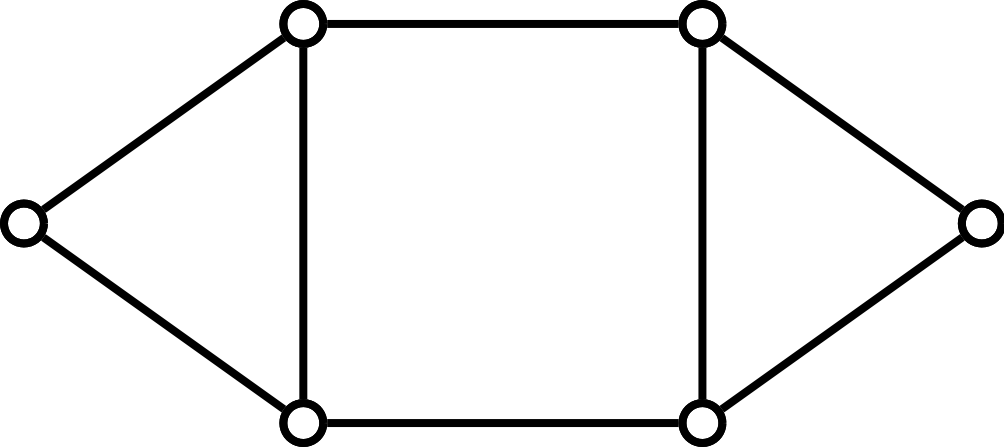
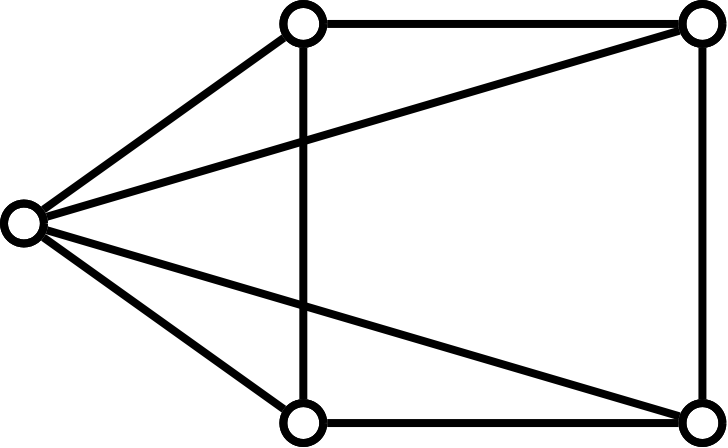
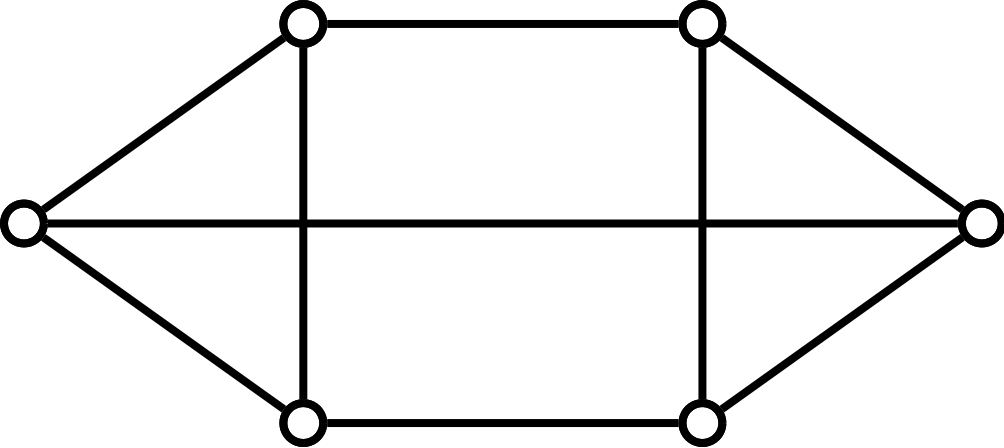
6.

Let \(e\) be any edge of \(K_n\text{.}\) Derive the chromatic polynomial of \(K_n\setminus e\) by colouring 'vertex by vertex'. Also find the chromatic polynomial of \(K_n/e\text{,}\) and then check that the deletion-contraction formula holds in this csae.

Now let \(f\neq e\) be another edge of \(K_n\text{.}\) What's the chromatic polynomial of \(K_n\setminus\{e,f\}\text{?}\) Does it matter whether \(e\) and \(f\) share a vertex?