Section 1.2 Degree and handshaking
Subsection 1.2.1 Definition of degree
Intuitively, the degree of a vertex is the “number of edges coming out of it”. If we think of a graph \(G\) as a picture, then to find the degree of a vertex \(v\in V(G)\) we draw a very small circle around \(v\text{,}\) the number of times the \(G\) intersects that circle is the degree of \(v\text{.}\) Formally, we have:
Definition 1.2.1.
Let \(G\) be a simple graph, and let \(v\in V(G)\) be a vertex of \(G\text{.}\) Then the degree of \(v\), written \(d(v)\text{,}\) is the number of edges \(e\in E(G)\) with \(v\in e\text{.}\) Alternatively, \(d(v)\) is the number of vertices \(v\) is adjacent to.
Example 1.2.2.
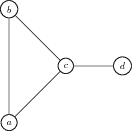
In the graph \(K\) shown in Figure 1.2.3, vertices \(a\) and \(b\) have degree 2, vertex \(c\) has degree 3, and vertex \(d\) has degree 1.
Note that in the definition we require \(G\) to be a simple graph. The notion of degree has a few pitfalls to be careful of \(G\) has loops or multiple edges. We still want to the degree \(d(v)\) to match the intuitive notion of the “number of edges coming out of \(v\)” captured in the drawing with a small circle. The trap to beware is that this notion no longer agrees with “the number of vertices adjacent to \(v\)” or the “the number of edges incident to \(v\)”
Example 1.2.4.
The graph \(G\) to the right has two vertices, \(a\) and \(b\text{,}\) and three edges, two between \(a\) and \(b\text{,}\) and a loop at \(a\text{.}\) Vertex \(a\) has degree 4, and vertex \(b\) has degree 2.
Subsection 1.2.2 Extended example: Chemistry
In organic chemistry, molecules are frequently drawn as graphs, with the vertices being atoms, and an edge betwen two vertices if and only if the corresponding atoms have a covalent bond between them (that is, they share a vertex).
Example 1.2.5. Alkanes.
The location of an element on the periodic table determines the valency of the element -- hence the degree that vertex has in any molecule containing that graph:
- Hydrogen (H) and Fluorine (F) have degree 1
- Oxygen (O) and Sulfur (S) have degree 2
- Nitrogen (N) and Phosphorous (P) have degree 3
- Carbon (C) has degree 4
Usually, most of the atoms involved are carbon and hydrogen. Carbon atoms are not labelled with a C, but just left blank, while hydrogen atoms are left off completely. One can then complete the full structure of the molecule using the valency of each vertex. On the exam, you may have to know that Carbon has degree 4 and Hydrogen has degree 1; the valency of any other atom would be provided to you
Graphs coming from organic chemistry do not have to be simple – sometimes there are double bonds, where a pair of carbon atoms have two edges between them.
Example 1.2.6.
If we know the chemical formula of a molecule, then we know how many vertices of each degree it has. For a general graph, this information is known as the degree sequence
Definition 1.2.7. Degree sequence.
The degree sequence of a graph is just the list (with multiplicity) of the degrees of all the vertices.
The following sage code draws a random graph with 7 vertices and 10 edges, and then gives its degree sequence. You can tweak the code to generate graphs with different number of vertices and edges, and run the code multiple times, and the degree sequence should become clear.
Knowing the chemical composition of a molecule determines the degree sequence of its corresponding graph. However, it is possible that the same set of atoms may be put together into a molecule in more than one different ways. In chemistry, these are called isomers. In terms of graphs, this corresponds to different graphs that have the same degree sequence.
An important special case is the constant degree sequence.
Definition 1.2.8. Regular graphs.
A graph \(\Gamma\) is \(d\)-regular, or regular of degree \(d\) if every vertex \(v\in\Gamma\) has the same degree \(d\text{,}\) i.e. \(d(v)=d\text{.}\)
As a common special case, a regular graph where every vertex has degree three is called trivalent, or cubic.
Some quick examples:
- The cycle graph \(C_n\) is two-regular
- The complete graph \(K_n\) is \((n-1)\)-regular
- The Petersen graph is trivalent
Subsection 1.2.3 Handshaking lemma and first applications
To motivative the Handshaking Lemma, we consider the following question. Suppose there seven people at a party. Is it possible that everyone at the party knows exactly three other people?
We can model the situation a graph, with vertices being people at the party, and an edge between two vertices if the corresponding people know each other. The question is then asking for the existence of a graph with seven vertices so that every vertex has degree three. It is then natural to attempt to solve the problem by trying to draw such a graph. After a few foiled attempts, we begin to suspect that it's not possible, but doing a case-by-case elimination of all the possibilities is daunting. It's easier to find a reason why we can't draw such a graph.
We will do this as follows: suppose that everyone at the party who knows each other shakes hands. How many handshakes will occur? On the one hand, from the definitions this would just be the number of edges in the graph. On the other hand, we can count the number of handshakes working person-by-person: each person knows three other people, and so is involved in three handshakes. But each handshake involves two people, and so if we count \(7*3\) we've counted each handhsake twice, and so there should be \(7*3/2=10.5\) handshakes happening, which makes no sense, as we can't have half a handshake. Thus, we have a contradiction, and we conclude such a party isn't possible.
Euler's handshaking Lemma is a generalization of the argument we just made to an arbitrary graph.
Theorem 1.2.9.
(Euler's handshaking Lemma)
Proof.
We count the “ends” of edges two different ways. On the one hand, every end occurs at a vertex, and at vertex \(v\) there are \(d(v)\) ends, and so the total number of ends is the sum on the left hand side. On the other hand, every edge has exactly two ends, and so the number of ends is twice the number of edges, giving the right hand side.
We have seen already seen one use of Euler's handshaking Lemma, but it will be particularly useful in Chapter 3, when we study graphs on surfaces.