Skip to main content

Section 5.2 Chromatic index and applications

It is a natural twist of the definition of chromatic number to try to colour the edges of a graph instead; the least number of colours needed is the called the chromatic index. After introducing this concept and giving some examples, we give some story problem type questions that boil down to finding either the chromatic number or chromatic index.

Definition 5.2.1. Chromatic index.

The chromatic index \(\chi^\prime(\bfG)\) of a graph \(\bfG\) is the least number of colours needed to colour the edges of \(\bfG\) so that any two edges that share a vertex have different colours.

Not that as with the chromatic number, since the chromatic index \(\chi^\prime(\bfG)\) is the minimum number of colours such that the edges can be coloured with adjacent edges having different colours, to show \(\chi^\prime(\bfG)=N\) typically requires two steps:

  1. Prove that the edges of \(\bfG\) can be coloured with \(N\) colours
  2. Prove that the edges of \(\bfG\) cannot be coloured with less than \(N\) colours

Let's find \(\chi^\prime(K_4)\text{.}\) Picking any vertex \(v\text{,}\) there are three edges incident to \(v\text{,}\) and none of these edges can have the same colour (as they all meet at \(v\)). Hence, we have \(\chi^\prime(K_4)\geq 3\text{.}\)

On the other hand, it is easy to colour the edges of \(K_4\) with three colours, as seen below, and so \(\chi^\prime(K_4)\leq 3\text{,}\) and hence \(\chi^\prime(K_4)=3\text{.}\)

Now, let's move on to \(K_5\text{.}\) Again, looking at any vertex we see all the edges adjacent to that vertex must be different colours, and so we have \(\chi^\prime(K_5)\geq 4\text{.}\) Let's try to colour the edges of \(K_5\) with 4 colours.

Suppose we coloured the four edges adjacent to the top vertex blue, green, red and purple, from left to right, and now look at the bottom edge. It is adjacent to edges coloured green and red, and so must be blue or purple. By symmetry, it's equivalent to colour it either colour, so let's suppose it's blue, giving us the following picture:

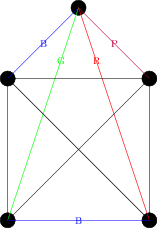
Now the edge on the right is adjacent to edges coloured red, blue and purple, and so must be green. But now we have a problem -- consider the edges labeled \(x\) and \(y\) in the next drawing:

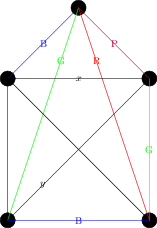
Both edges share vertices with edges coloured green, blue, and purple, and hence each would need to be coloured red. But they also share a vertex with each other, and so cannot both be coloured red. So we see \(\chi^\prime(K_5)\geq 5\text{.}\)

On the other hand, it is easy to colour the edges of \(K_5\) with 5 colours: colour each edge in the outside pentagon a different colour. For each edge in the outside pentagon there will be a unique edge in the inside star that does meet that edge (the one "parallel" to it) -- draw that edge the same colour. That results in the following colouring:

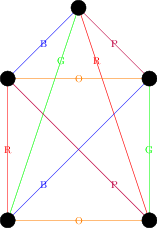
In the examples above, we found lower bounds for \(\chi^\prime(\bfG)\) by considering the degrees of vertices; this argument easily adapts in general.

Let \(v\in\bfG\) be a vertex of maximal degree \(d(v)=\Delta(\bfG)\text{.}\) Then none of the \(\Delta(\bfG)\) edges incident to \(v\) can be coloured the same colour, and so we have \(\chi^\prime(\bfG)\geq \Delta(\bfG)\)

It turns out that this nearly determines the chromatic index \(\chi^\prime(\bfG)\) -- it can be at most one more than \(\Delta(\bfG)\text{:}\)

The lower bound was just proved in the previous theorem. The other direction is more difficult.

We now show how determining the chromatic number and chromatic index can show up as part of story questions.

Suppose there are six friends, Alice, Bob, Charlie, Dora, Elizabeth and Frank, and there is the following graph between then:

A
X B
X C
X X D
X X E
X X X F

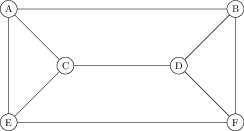
Here are two word problems related to \(\bfG\text{:}\)

  1. The friends want to divide into groups, but the edges indicate people who currently annoy each other. What's the least number of groups the friends can divide into groups so that no group contains two people who annoy each other?
  2. The friends want to hold a snooker tournament, with everyone playing three matches; the edges indicate pairs of friends who will play against each other. If multiple matches can be played each day, but each person can only be involved in one match a day, how many days are necessary to hold the tournament?

The first case concerns the chromatic number -- each group of people will be the people who have the same colour, and we don't want vertices with an edge between them to have the same colour.

The second case concerns the chromatic index -- the edges are the games that are being played, and all edges that are the same colour will be played on the same day.

Let us quickly compute the chromatic number and chromatic index of the graph \(\bfG\) above. To compute the chromatic number, we observe that the graph contains a triangle, and so the chromatic number is at least 3. But it is easy to colour the vertices with three colours -- for instance, colour A and D red, colour C and F blue, and colur E and B green. So \(\chi(\bfG)=3\text{.}\)

To compute \(\chi^\prime(G)\text{,}\) since \(A\) has degree three we have \(\chi^\prime(\bfG)\geq 3\text{.}\) On the other hand, it is easy to colour the edges with three colours -- for instance, colour AB, CE and DF red, colour AE, CD and BF blue, and colour AC, BD and EF green. So \(\chi^\prime(\bfG)=3\) as well.