Section 4.1 Introduction to Graphs on Surfaces
We begin our study of graphs on surfaces with an old chestnut of a problem, the solution of which we will develop into a more general algorithm.
Subsection 4.1.1 The Utilities Problem
Suppose there are three houses, owned by Alice, Bob, and Carol, and they'd each like to be connected to one of three Utilities, say, gas, electricity, and water. There is no real difficulty in the real world, but if we add the restriction that we don't want any of the lines to cross over or under each other, the problem becomes quite interesting. A failed attempt at drawing a solution is shown here.
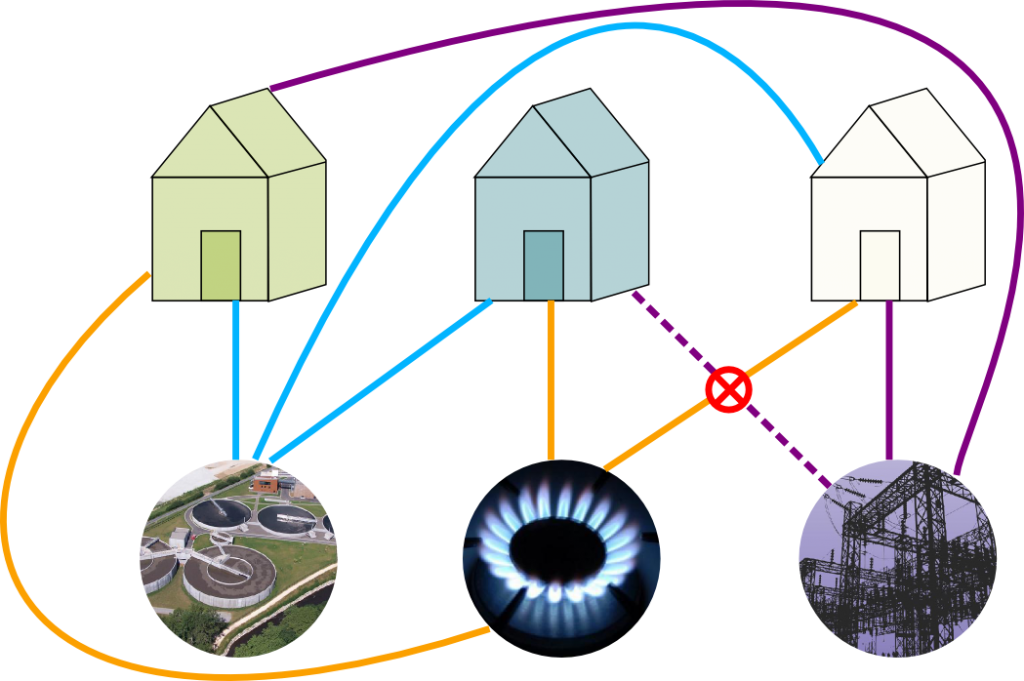
Although this attempt failed, it seems very difficult to rule out that some other attempt wouldn't succeed; trying to make a case by case argument seems quite difficult to organize, and it's not clear that there are even finitely many possibilities. We need a careful way to approach the problem, which we will do in a moment, but first we will use this problem as motivation to make a few definitions.
Subsection 4.1.2
Definition 4.1.2.
A graph is planar if it can be drawn on a piece of paper so that no edges cross.
That definition is a bit loose -- for instance, it's left implicit, we're drawing the edges as lines, with the endpoints being the two vertices it connects. But this will be strong enough for our purposes.
With this definition in hand, the Utilities Question is asking whether the graph \(K_{3,3}\) is planar -- treat the three utilities as red vertices, say, and the three houses as the blue vertices. This doesn't really help us organize our proof, however. To do that, we will use the basic fact that any circle drawn on the plane has an inside and an outside.
This last fact sounds absolutely trivial, but first, it is not true on other surfaces, for instance, on the torus -- in our video game world, the top of the screen makes a circle, but a point just above this circle is really at the bottom of the video game world, and so the circle doesn't cut the torus into two pieces; I also illustrated this with the Mobius band: the central line down the middle doesn't separate it into two pieces. This fact is usually stated as follows:
Theorem 4.1.3. Jordan Curve Theorem.
Any simple closed plane curve has an interior and an exterior
Though easy to state, and intuitively obvious, the Jordan Curve Theorem is surprisingly subtle and difficult to prove; we won't use any more topology than this.
Before seeing it in practice, let's discuss informally how the Jordan Curve Theorem can be used to help prove whether a graph \(G\) is planar or not. Suppose that we have found a large cycle \(C_k\) as a subgraph of \(G\text{.}\) Then, if we had a planar drawing of \(G\text{,}\) this cycle would have to appear as a circle. By the Jordan Curve Theorem, this circle would have an inside and an outside, and every vertex and edge not in our cycle \(C_k\) would have to be either entirely within the circle, or entirely outside the circle. This gives us a way to organize the case by case argument.
The bigger a cycle we can find, the fewer other vertices and edges we need to consider, and so we have a much cleaner case by case argument. In the best cases, the graph is Hamiltonian and the cycle \(C_k\) includes all the vertices of \(G\text{,}\) and we only have to do a case by case analysis for some the remaining edges.
Let's see how this general principle gets illustrated in practice
Theorem 4.1.4.
\(K_{3,3}\) isn't planarProof.
First let's name the vertices of \(K_{3,3}\text{:}\) let the vertices \(a,b,c\) be the blue circle vertices, and \(x,y,z\) be the red rectangle vertices. Then the path \(a-x-b-y-c-z-a\) is a Hamiltonian cycle, and so if \(K_{3,3}\) were planar it would be drawn as a circle in the plane, as shown below:
This contains 6 of the 9 edges of \(K_{3,3}\text{;}\) we need to add the edges \(a-y, b-z\) and \(c-x\text{.}\) The edge \(a-y\) could be drawn inside the circle or outside, suppose we draw it inside, as shown below, with the added edge dashed.
Then on the inside of the circle, \(x\) and \(c\) are on different sides of the line \(a-y\text{,}\) and so the edge connecting them must go outside the circle. The added edge could go around the right of the circle, as shown below here:
or around the left, as shown here:
But now \(b\) and \(z\) are different sides of \(a-y\) inside the circle, and on different sides of \(c-x\) outside the circle, and so cannot be connected without making two edges cross.
If we had began by drawing \(a-y\) outside the circle, then we would have had to draw \(c-x\) inside the circle, and had the same problem with being able to draw the last line; as shown here: