Skip to main content

Section 1.3 Graph Isomorphisms

Generally speaking in mathematics, we say that two objects are "isomorphic" if they are "the same" in terms of whatever structure we happen to be studying. The symmetric group \(S_3\) and the symmetry group of an equilateral triangle \(D_6\) are isomorphic. In this section we briefly briefly discuss isomorphisms of graphs.

Subsection 1.3.1 Isomorphic graphs

The "same" graph can be drawn in the plane in multiple different ways. For instance, the two graphs below are each the "cube graph", with vertices the 8 corners of a cube, and an edge between two vertices if they're connected by an edge of the cube:

Figure 1.3.1. Two drawings of the cube graph

It is not hard to see that the two graphs above are both drawings of the cube, but for more complicated graphs it can be quite difficult at first glance to tell whether or not two graphs are the same. For instance, there are many ways to draw the Petersen graph that aren't immediately obvious to be the same.

This animated gif created by Michael Sollami for this Quanta Magazine article on the Graph Isomorphism problem illustrates many different such drawings in a way that makes the isomorphisms apparent.

Definition 1.3.3.

An isomorphism \(\varphi:G\to H\) of simple graphs is a biject \(\varphi:V(G)\to V(H)\) between their vertex sets that preserves the number of edges between vertices. In other words, \(\varphi(v)\) and \(\varphi(w)\) are adjacent in \(H\) if and only if \(v\) and \(w\) are adjancent in \(G\text{.}\)

Figure 1.3.5. \(C_5\) is isomorphic to its complement \(C_5^c\)

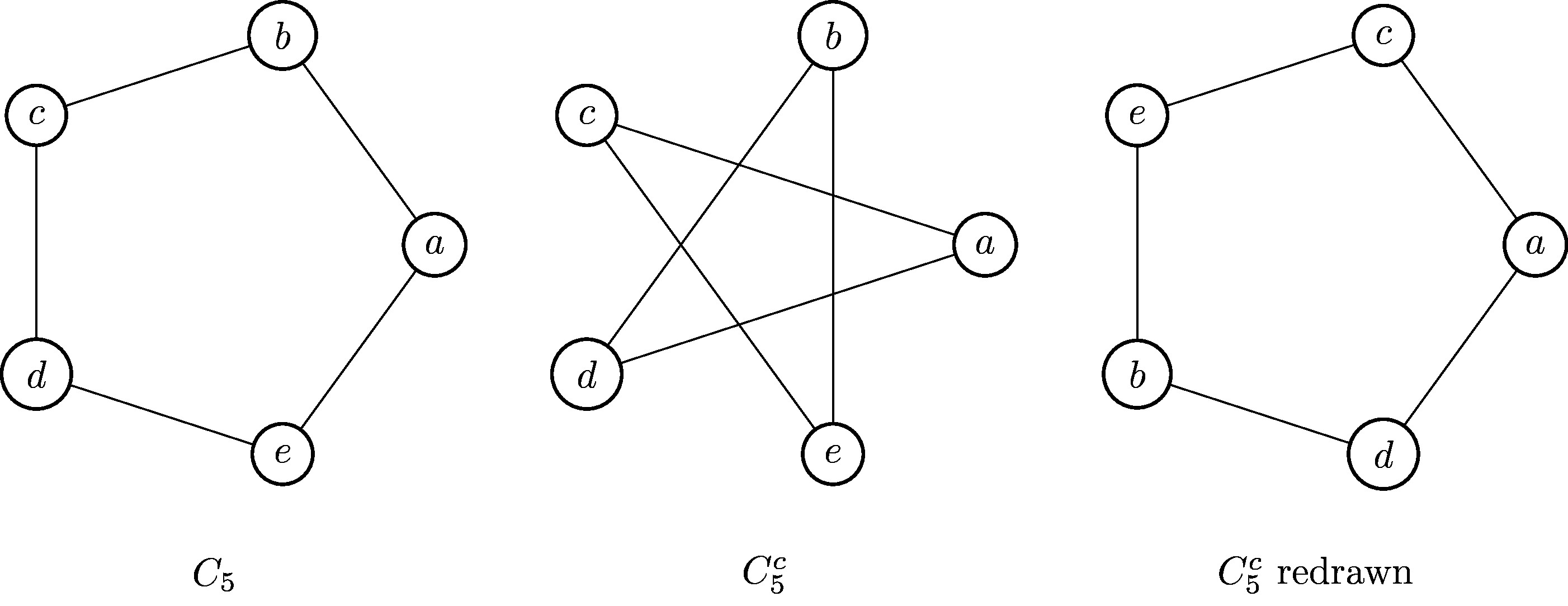
The cycle graph on 5 vertices, \(C_5\) is isomorphic to its complement, \(C_5^c\text{.}\) The cycle \(C_5\) is usually drawn as a pentagon, and if we were then going to naively draw \(C_5^c\) we would draw a 5-sided star. However, we could draw \(C_5^c\) differently as shown, making it clear that it is isomorphic to \(C_5\text{,}\) with isomorphism \(\varphi:C_5\to C_5^c\) defined by \(\varphi(a)=a, \varphi(b)=c, \varphi(c)=e, \varphi(d)=b, \varphi(e)=d\text{.}\)

Although solving the graph isomorphism problem for general graphs is quite difficult, doing it for small graphs by hand is not too bad and is something you must be able to do for the exam. If the two graphs are actually isomorphic, then you should show this by exhibiting an isomrophism; that is, writing down an explicit bijection between their vertex sets with the desired properties. The most attractive way of doing this, for humans, is to label the vertices of both copies with the same letter set.

If two graphs are not isomorphic, then you have to be able to prove that they aren't. Of course, one can do this by exhaustively describing the possibilities, but usually it's easier to do this by giving an obstruction – something that is different between the two graphs. One easy example is that isomorphic graphs have to have the same number of edges and vertices. We'll discuss some others in the next section

Subsection 1.3.2 Heuristics for showing graphs are or aren't isomorphic

Another, only slightly more advanced invariant is the degree sequence of a graph that we saw last lecture in our discussion of chemistry.

If \(\varphi:G\to H\) is an isomorphism of graphs, than we must have \(d(\varphi(v))=d(v)\) for all vertices \(v\in G\text{,}\) and since isomorphisms are bijections on the vertex set, we see the degree sequence must be preserved. However, just because two graphs have the same degree sequences does not mean they are isomorphic.

Slightly subtler invariants are number and length of cycles and paths.

Subsection 1.3.3 Cultural Literacy: The Graph Isomorphism Problem

This section, as all "Cultural Literacy" sections, is information that you may find interesting, but won't be examined.

The graph isomorphism problem is the following: given two graphs \(G\) and \(H\text{,}\) determine whether or not \(G\) and \(H\) are isomorphic. Clearly, for any two graphs \(G\) and \(H\text{,}\) the problem is solvable: if \(G\) and \(H\) both of \(n\) vertices, then there are \(n!\) different bijections between their vertex sets. One could simply examine each vertex bijection in turn, checking whether or not it maps edges to edges.

The problem is interesting because the naive algorithm discussed above is not very efficient: for large \(n\text{,}\) \(n!\) is absolutely huge, and so in general this algorithm will take a long time. The question is, is there are a faster way to do check? How fast can we get?

The isomorphism problem is of fundamental importance to theoretical computer science. Apart from its practical applications, the exact difficulty of the problem is unknown. Clearly, if the graphs are isomorphic, this fact can be easily demonstrated and checked, which means the Graph Isomorphism is in NP.

Most problems in NP are known either to be easy (solvable in polynomial time, P), or at least as difficult as any other problem in NP (NP complete). This is not true of the Graph Isomorphism problem. In November of last year, Laszlo Babai announced a quasipolynomial-time algorithm for the graph isomorphism problem – you can read about this work in this great popular science article.